38 两个有趣的问题

两个有趣的问题(一)

问题栈和队列在实现上非常相似，是否可以用栈实现队列?
问题分析用栈实现队列等价于用“后进先出”的特性实现“先进先出”的特性!
解决方案设计
实现思路
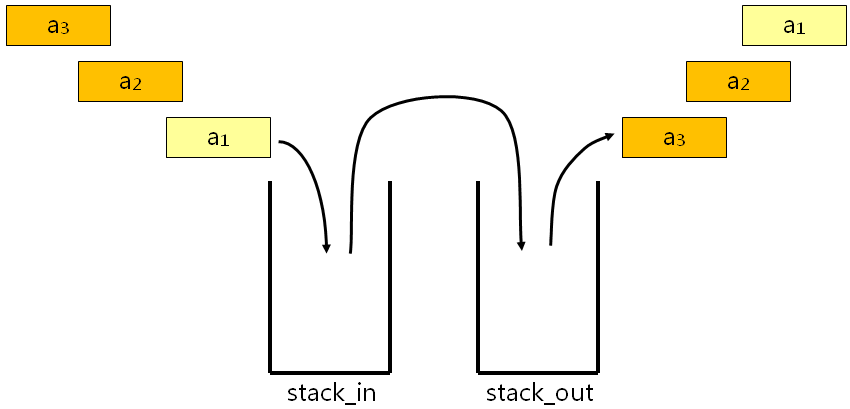
- 准备两个栈用于实现队列:stack_in和stack_out
  - 当有新元素入队时:将其压入stack_in
  - 当需要出队时:
    - stack_out.size() == 0:
      - 将stack_in中的元素逐一弹出并压入stack_out
      - 将stack_out的栈顶元素弹出
    - static_out.size()>0:
      - 将stack_out的栈顶元素弹出

编程实验

用栈实现队列

#ifndef STACK2QUEUE_H
#define STACK2QUEUE_H

#include <LinkedStack.h>
#include <Queue.h>

namespace KylinLib {
template<typename T>
class Stack2Queue : public Queue<T>{
public:
    virtual void add(const T &value){
        m_in.push(value);
    }
    virtual void remove(){
        if(size()<=0)
            THROW_EXCEPTION(InvalidOperationException,"There is no element in the queue...");
        if(m_out.size()<=0){
            while (m_in.size()>0) {
                m_out.push(m_in.top());
                m_in.pop();
            }
        }
        m_out.pop();
    }
    virtual T& front() {
        if(size()<=0)
            THROW_EXCEPTION(InvalidOperationException,"There is no element in the queue...");
        if(m_out.size()<=0){
            while (m_in.size()>0) {
                m_out.push(m_in.top());
                m_in.pop();
            }
        }
        return m_out.top();
    }
    virtual void clear(){
        m_in.clear();
        m_out.clear();
    }

    virtual size_t size() const {
        return m_in.size()+m_out.size();
    }

private:
    LinkedStack<T> m_in;
    LinkedStack<T> m_out;
};
}
#endif // STACK2QUEUE_H

两个有趣的问题(二)

问题反之，是否可以用队列实现栈？
问题分析本质为，用队列“先进先出”的特性实现栈“后进先出”的特性！
解决方案设计
实现思路
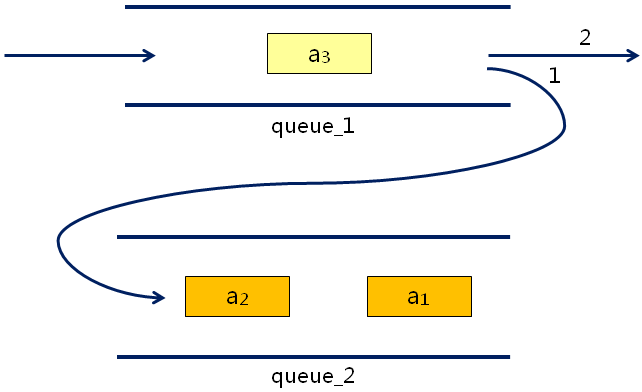
- 准备两个队列用于实现栈:queue_1[in]和queue_2[out]
  - 当有新元素入栈时:将其加入队列[in]
  - 当需要出栈时:
    - 将队列[in]中的n-1个元素出队列，并进入队列[out]中
    - 将队列[in]中的最后一个元素出队列(出栈)
  - 交换两个队列的角色:queue_1[out]和queue_2[in]

编程实验

用队列实现栈

#ifndef QUEUE2STACK_H
#define QUEUE2STACK_H

#include "LinkedQueue.h"
#include "Stack.h"

namespace KylinLib {
template<typename T>
class Queue2Stack:public Stack<T>{
public:
    virtual void push(const T &value){
        auto &m = m_oneIn?m1:m2;
        m.add(value);
    }

    virtual void pop() {
        if(size()<=0)
            THROW_EXCEPTION(InvalidOperationException,"There is no element in stack...");
        auto &in = m_oneIn?m1:m2;
        auto &out = m_oneIn?m2:m1;
        if(out.size()>0)
            out.remove();
        else {
            while (in.size()>1) {
                out.add(in.front());
                in.remove();
            }
            m_oneIn = !m_oneIn;
            in.remove();
        }

    }
    virtual T& top(){
        if(size()<=0)
            THROW_EXCEPTION(InvalidOperationException,"There is no element in stack...");
        auto &in = m_oneIn?m1:m2;
        auto &out = m_oneIn?m2:m1;
        if(out.size()>0)
            return out.front();
        else {
            while (in.size()>1) {
                out.add(in.front());
                in.remove();
            }
            m_oneIn = !m_oneIn;
            return in.front();
        }
    }

    virtual void clear() {
        m1.clear();
        m2.clear();
    }

    virtual size_t size()const {
        return m1.size()+m2.size();
    }
private:
    LinkedQueue<T> m1;
    LinkedQueue<T> m2;
    bool m_oneIn = true;
};
}

#endif // QUEUE2STACK_H

小结

栈和队列在实现上非常类似，可以相互转化实现
两个栈“后进先出”叠加得到“先进先出”的特性
两个队列“先进先出”相互配合得到“先进后出”的特性
栈和队列相互转化的学习有助于强化本质的理解

两个有趣的问题(一)​

编程实验​

两个有趣的问题(二)​

编程实验​

小结​

两个有趣的问题(一)

编程实验

两个有趣的问题(二)

编程实验

小结